|
|
||||||||||||||||||||
 |
(b)ラグビーセンサの姿勢とその表現 ラグビーセンサの姿勢について考える前に,ラグビーセンサに図1.2のような1つの直交座標系を固定する。 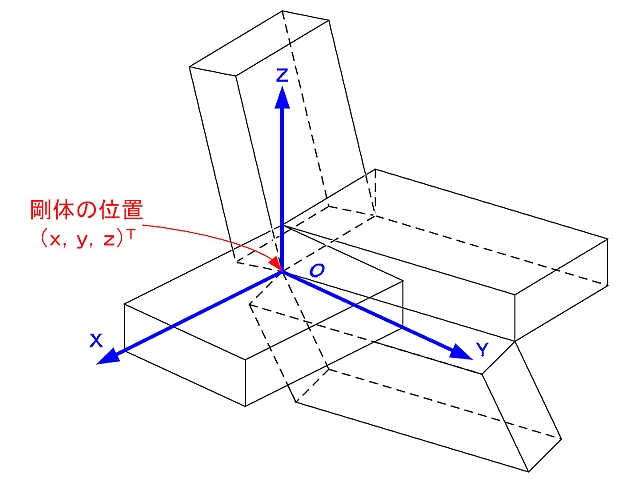 原点の取り方は任意であるが,ここではラグビーセンサの代表点,すなわちラグビーセンサの位置を表す粒子の位置を原点とし、o-xyz座標系をとる。より具体的には、ラグビーセンサの基板に搭載した加速度センサチップの中央をその原点とする。この座標系はラグビーセンサと一緒に運動し、ラグビーセンサ座標系(センサー座標系)とも呼ばれる。 ラグビーセンサが存在する3次元空間にも基準になる座業系が固定されているとする。 この座標系をO-XYZとする。この座標系を絶対座業系(グランド座標系)とよぶことがあるが,力学的には慣性座標系の1つである。慣性座標系は,空間に静止しているか,等速直線運動をしている座標系である。 ラグビーセンサの姿勢とは,o-xyzがO-XYZから見てどのように傾いているかを表している。ラグビーセンサの位置とは,O-XYZでみたo-xyzの原点の位置である。 センサー座標系のx軸,y軸,z軸のそれぞれに、原点を始点する単位ベクトルex,ey,ezを貼り付ける。これらのベクトルの各成分はO-XYZで表されるとする。 3個の単位ベクトルをx,y,zの順番に並べて、次のような3×3の行列Rを作る。 R=(ex,ey,ez) (1.1.1) このようにして作ったRは直交行列となる,直行行列とは転置行列が逆行列になる行列である。 直交行列は行列式が+1になるものと-1になるものの2つに分類される。O-XYZとo-xyzが共に右手座標系(あるいは共に左手座標系)の場合には,行列式は必ず+1をとる。行列式が+1になるものの集合をSO(3)と記す。 これは「エス・オー・スリー」と読み,数学の群論では3次の特殊直交群と呼ばれる。 すなわち、 RT=R-T, detR=1 ←→ R € SO(3) (1.1.2) O-XYZが右手系でo-xyzが左手系である場合,直交行列Rの行列式は-1となる。このように右手座標系から左手座標系へ,あるいはその逆へと座標系の取り方を変更する場合に,行列式が-1となるのである。 ラグビーセンサの姿勢が変化する場合,Rの9個の成分は変化する。したがって,Rをラグビーセンサ姿勢の数学的な表現と考えることができる。 ただし,Rの各列ベクトルの大きさは1である。すなわち exTex=eyTey=ezTez=1 (1.1.3) である。また列ベクトルは互いに直交する。すなわち exTey=eyTez=ezTex=0 (1.1.4) である。 上の2式はそれぞれ3個ずつの拘束条件をもっている。したがって,ラグビーセンサの姿勢の変化に伴っての変化するRの9つの成分のうちで,独立なものの数は3となる。 ラグビーセンサの姿勢の運動の自由度,すなわちラグビーセンサの姿勢の集合の次元が3になることを1つの数式表現で具体的に表したものである。 ここでは3自由度のラグビーセンサの姿勢の空間を9変数と6個の拘束条件で表しているが,同じものを拘束条件の無い3変数のみで表せないだろうか? これはラグビーセンサ姿勢の3次元空間に3本の座標のメモリを描き,1つのラグビーセンサ姿勢を1組の座標値で表せないかという問いである。 答えは,・・・ 否である。 ラグビーセンサ姿勢の空間全体を3変数で表すことがきない。3変数で表そうとすると,ラグビーセンサ姿勢の空間の必ずどこかにそれらの変数では一対一で表現できない場所が生まれる。 このような場所を特異点という。 特異点の周辺でも表現上の歪が生じることにもなる。 これは,つぎのようなアナロジーで説明されている。 球面は2次元の曲面であるが,これを2個の座標値であらわそうとすると困難な問題が生じる。 つまり世界地図を描く問題である。いろいろな世界地図が考え出されているが,いずれも一長一短にで,地球儀をまったく不便なく紙の上に描くことはできない。 よく知られているメルカトール図法では,点であるはずの北極点,南極点がそれぞれ線の広がりをもつ。 これが一対一で表せない特異点である。また,南極大陸やシベリアが地球儀の上で見るよりも歪み,極端に拡大されて表される。 ラグビーセンサの位置が3次元ユークリッド空間で表され,x、y、zの3変数で問題なく表すことができたのに対して,ラグビーセンサ姿勢が上述のような表現の問題をもつことは特筆すべきことである。 ラグビーセンサの姿勢の表現として次のようなものがある。
直交行列による姿勢の表現は,物理的に理解しやすく,数学的にも扱いやすい表現である。ラグビーセンサ姿勢の空間全体を表現する方法として,もっとも自然であるといえる。ただし,6個の余分な変数を含むことが欠点である。 オイラー角は,ラグビーセンサ姿勢を3変数で表そうとするものである。ラグビーセンサ姿勢の空間全体を表すことができず,特異点などの問題があるため,便宜的表現であるといわざるをえない。それでも余分な変数を使わずに表現できることが便利なため,採用されることが多い。 オイラーパラメータあるいはクォータニオン(四元数)とよばれる表現法がある。 これはラグビーセンサ姿勢の空間全体を表現するもう1つの方法である。この表現では4変数と1個の拘束条件を用いてラグビーセンサの姿勢を表す。 ラグビーセンサ姿勢の空間全体を最小の変数で表す表現である。 オイラーパラメータ,あるいは,クォータニオンの演算がやや複雑で特殊なことが問題である。ロケットや人工衛星の姿勢制御で広く採用されている。 |
||||||||||||||||||||
|
(C)直交行列の性質 ラグビーセンサ姿勢の運動の性質はSO(3)の性質を調べることで,自然に明らかになる。 素直な数学的表現が物理の本質を垣間見せるとも言えるだろう。 [性質1]:R€SO(3) RєSO(3)よりRT=R-1,detR=1,逆もまた真である。 Rの成分を以下にように表す。  このとき,rijに対する余因子をRijとおくならば rij=Rij (1.1.6) である。余因子とはn次の正方行列Mに対して,i行とj行を消し去ったn-1次の正方行列Mijとおくとき,Δij=(-1)i+jdetMijのことである。 Δijを(i,j)要素とするn次正方行列MはMの余因子行列と呼ばれる。 Mが正則ならば,一般に逆M-1=1/detM M と計算できる。これをRに当てはめれば, R-1=1/detR Ř =RT (1.1.7) となる。ここでdetR=1を使い,上式の右辺と中辺の各成分を比べると,上述の結果を得る。これはn×nの直交行列R(n)€Rである。 R(n)€SO(n)の特性多項式は次のようになる。 F(λ)=det{R(n)-λE} =(-λ)n+c1(-λ)n-1+c2(-λ)n-2+・・・+cn-1(-λ)+cn = 0 (1.1.8) ここで,Eは単位行列である。この多項式の根がR(n)の固有値である。 cn=detR(n)=1である。また上の性質2より,ci=cn-i(i=1,・・・,n-1)となる。このような性質をもつ多項式を逆数方程式とよぶことがある。なぜなら,λが解ならλ-1もまた解となるからである。 Rに対して以下の式が成り立つ。 det(R-λE) =(-λ)3+(r11+r22+r33)(-λ)2+(r11+r22+r33)(-λ)1+1 = 0 (1.1.9) R(n)€SO(3)ならば,またはRN(n)€SO(n)でもある。ここでNは整数であり,RN(n)はR(n)のN乗である。これは性質1を用いて確認することができる。R(n)の固有値をλk(k=1,・・・,n)とすると,RN(n)の固有値はλkN(k=1,・・・,n)と表すことができる。固有値は複素数の場合もある。すべての固有値の積が行列式であり,両方の直交行列に対してこれは1に等しい。また,固有値の総和は行列の対角要素の和,すなわちトレースに等しい。 したがって, traceR(n)=Σλk (1.1.10) traceRN(n)=ΣλkN (1.1.11) 直交行列の各列の単位ベクトルであるから,対角要素の絶対値はたかだか1である。 したがって, |traceRN(n)|=|ΣλkN|≤n (1.1.12) となる。 大きなNに対して,これらの関係がすべて満たされるためには,|λk|=1(k=1,・・・,n)でなければならない。 これよりR(n)のすべての固有値の絶対値は1であることがわかる。 上述の性質3と性質4よりR(n)の固有値は, nが偶数 ---> e±iφj (j=1,・・・,n/2) (1.1.13) nが奇数 ---> e±iφj (j=1,・・・,n-1/2) (1.1.14) となる。ここで,i2=-1である。したがって、R€SO(3)は,1,e±iφを固有値とする。 Rは固有値1をもつ。 これに対する固有ベクトルは 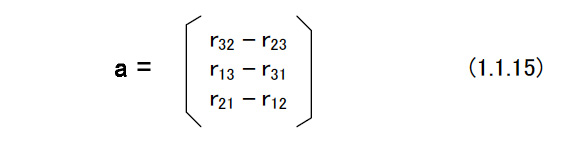 である。これは性質2を用いて以下の計算することによって容易に示すことができる。 Ra =a (1.1.16) 左辺はベクトルaをRが示す量だけ回転させることを表している。上式はaがRによる回転によって不変なベクトル,すなわち回転軸であることを表している。 固有値e-iφに対する固有ベクトルをp+iqとおくと,p-iqが固有値eiφの固有ベクトルになることが直ちにわかる。直交行列を含むユニタリ行列で固有値がすべて異なるときには,固有ベクトルは直交することが知られている。Rでは,3個の固有値がすべて1であるときを除けば,固有値はすべて異なる。これらが直交することから |p|=|q| (1.1.17) p⊥q,a⊥p,a⊥q (1.1.18) となる。a,p,qをそれぞれ正規化したものをe1,e2,e3とおくと次のようになる。 Re1=e1 (1.1.19) R(e2+ie3)=e-iφ(e2+ie3) (1.1.20) 実部,虚部をそれぞれ比較し,Ro=(e1 e2 e3)€ SO(3) を用いて上式をまとめると次のようになる。 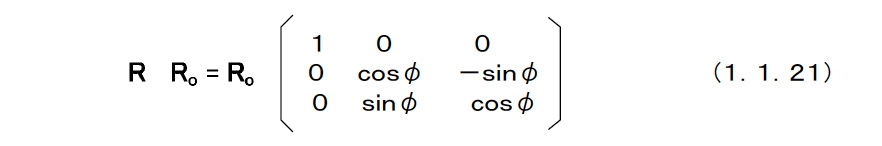 これから以下の式が得られる。 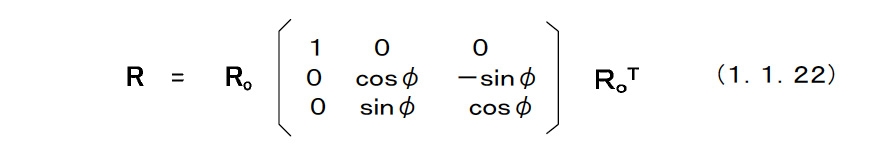 (1.1.22)式はRが,直行行列による相似変換によって,必ずx軸周りの大きさφの回転という正準形に変換できることを表している。 正方行列のトレースが固有値の総和であることから traceR=1+eiφ+e-iφ=1+2cosφ (1.1.23) 性質2および(1.1.23)式を用いると,(1.1.15)式から次の式が得られる。 |a|2=3+2traceR-(traceR)2=4sin2φ (1.1.24) 1点を固定されたラグビーセンサの変位は,固定された軸周りの1回の回転で表すことができる。これをオイラーの定理という。(1.1.22)式はRが表すラグビーセンサ姿勢の変位,つまり1点を固定されたラグビーセンサの変位が,軸a周りの,おおきさφの回転で表すことができることを示している。 これはRが必ず固有値1を持つことに起源していることに注意する。 |
||||||||||||||||||||
|
(d)直交行列を用いた演算 図1.3に示すような2つのラグビーセンサ姿勢がある。 これらを座標系{A}と{B}で表す。 グランド座標系を{O}として,2つの座標系の姿勢を「{O}からみた{A}」,「{O}からみた{B}」という意味で,次のように書くことにする。 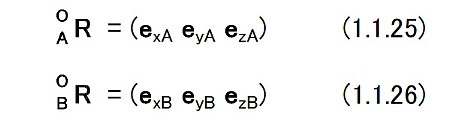 これを相対姿勢という。 上の式でexAは座標系{A}のx軸方向を向く単位ベクトルである。 6個の単位ベクトルは,成分がすべてグランド座標系で表されたものであることに注意する。 座標系{A}から見た座標系{B}をBARとすれば,これは相対的なラグビーセンサ姿勢の変位を表す。 これを表現するためには{B}の3個の単位ベクトルの,{A}の各軸への方向余弦を計算すればよい。 したがって,次のようになる。 図1.3 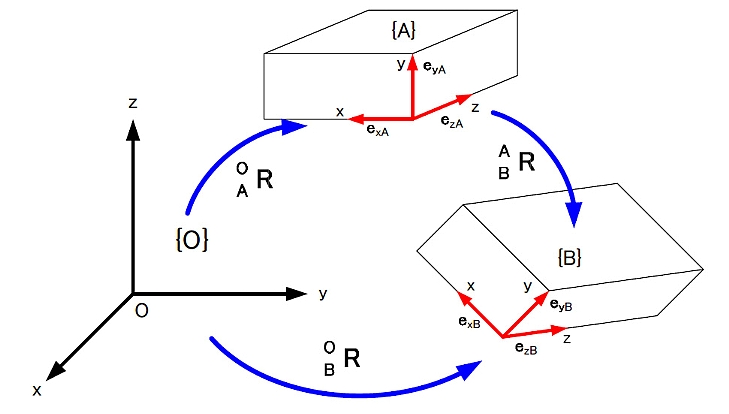 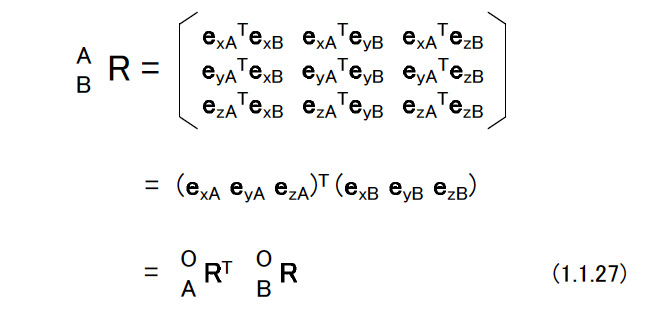 このようにRはラグビーセンサの回転を表したり,相対的な姿勢の変化を表したりすることから,回転行列あるいは姿勢変換行列とよばれることがある。 (1.1.27)式においてBARの要素を以下のようにする。 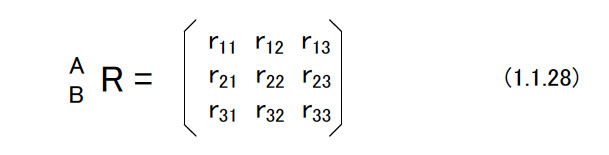 座標系{A}を座標系{B}に一致させるためには,座標系{A}に対して 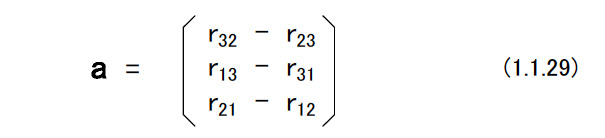 を軸として,(1.1.23)式および(1.1.24)式が与えるφを回転の大きさとする1回の回転を行えばよい。aは座標系{A}と座標系{B}の絶対姿勢,すなわちAORとBORから次のようにして計算することができる。 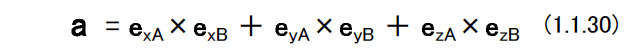 (1.1.27)式と同様に考えると{B}から見た{A},すなわちABRは 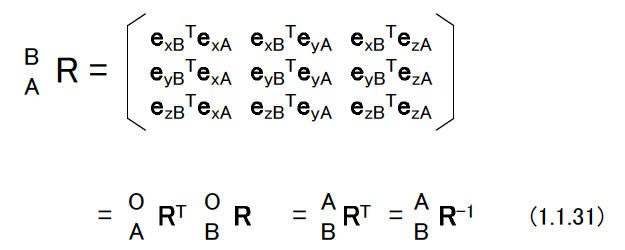 となる。この関係を用いると(1.1.27)式は次のように書くことができる。 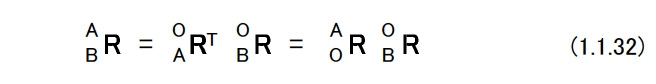 これを一般化すると重要な計算則が得られる。 n個の座標系{1},・・・,{n}があるとしよう。このとき, 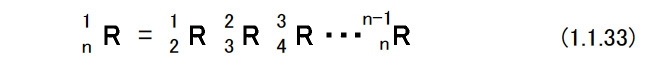 となる。 これを(鎖状則)とよばれる。 {1}→{2},{2}→{3},{3}→{4}というように,相対的な姿勢の変位を表す直交行列を左から右へ掛けてゆくことによって{1}→{n}の姿勢の変位を計算することができる。 グランド座標系{O}と座標系{A}がある。 ベクトルxに対して,次のような演算を行う。 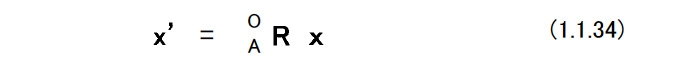 この意味を考えてみよう。 もしxが{A}で記述されたベクトルなら,x’は同じベクトルを{O}で記述したもの,つまり座標系の変換を意味している。 物理的にはxとx’は同じベクトルであるが,成分表示する座標系が変わったという解釈になる。 重力加速度gを考えると,gが{A}で計測された(記述された)重力ベクトルであれば,g’は同じ重力ベクトルを{O}で記述したものでその値は,z軸方向にgの値を持つ。 もしxが{O}で記述されたベクトルなら,少し物理的な意味が変わってくる。 図1.4のように,初期時刻においてラグビーセンサは{A}と{O}と一致した姿勢をしていたと考えよう。 図1.4 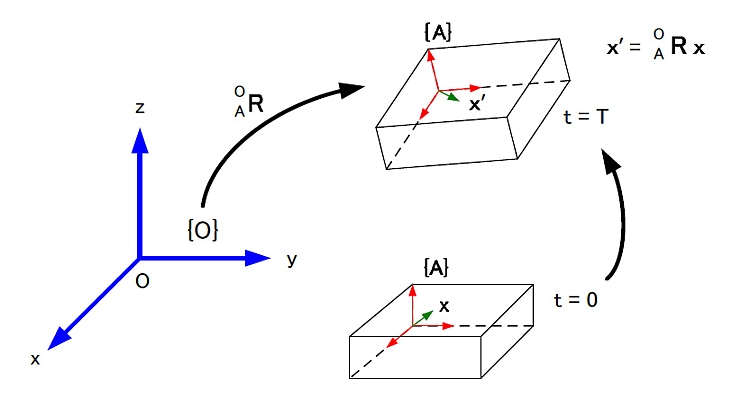 このとき座標系{O}で成分表示されたベクトルxがラグビーセンサに固定され,時間と共にラグビーセンサの姿勢は変化してAORとなった。 これによって,ラグビーセンサに固定されていたベクトルはラグビーセンサと共に回転して新たな方向を持った。 これがx’である。 この場合にはxとx’は物理的に異なるベクトルであり,上式はベクトルの回転を表していると解釈できる。 後者の場合で,回転後のベクトルxをラグビーセンサに固定された座標系で成分表示したものは,回転前のxの{O}による成分表示と等しい。 したがって,前者と後者の物理的な意味は異なっているが、数学的にはおなじものである。 |
||||||||||||||||||||
| (e)オイラー角 オイラー角はラグビーセンサの姿勢を3個の変数,(α,β,γ)で表現しようとする。 さまざまな問題が生じる(特異解の存在)が,最小の変数でラグビーセンサの姿勢を表せることは便利なことが多いため,使ってみる。 オイラー角の3つの角度の定義は,いくつかの異なるものがあるが,典型的なものを図1.5に示す。 図1.5 Z-Y-Zオイラー角
このオイラー角は回転軸の順番からZ-X-Zオイラー角と呼ばれる。 z軸→y軸→x軸の順番で回転させたものは,同様にZ-Y-Xオイラー角と呼ばれる。 x、y、zの各軸周りに角度θだけ回転する場合のRをそれぞれRX(θ),RY(θ),RZ(θ)と書くと,それらは次のようになる。 |
|||||||||||||||||||||
|
1.2ラグビーセンサの運動 (a)角速度ベクトル ラグビーセンサの位置と姿勢が時間と共に変化する場合の問題を考える。 運動中のラグビーセンサの姿勢がある時刻にRとなったと考える。 Rは直交行列であるから RRT = E (1.2.1) である。Rは時間と共に変化するかが,単位行列Eは変化しない。したがって,上式を微分すると次の式が得られる。 Ω + ΩT = 0 (1.2.3) これは,Ωが交代行列(AT=-Aを満たす行列,歪対称行列ともいう)であることを意味する。よってΩは次のように表すことができる。 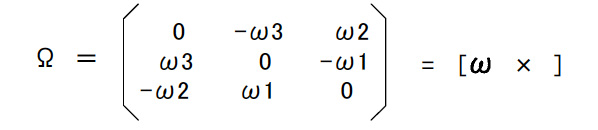 (1.2.4)
(1.2.4)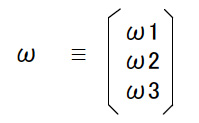 (1.2.5) (1.2.5)上式のωは角速度ベクトル,あるいは単に角速度と呼ばれる。この物理量はRの運動の結果として現れる交代行列Ωの非対角成分からつくられるものである。 外積は,奇妙な演算である。外積が定義できるのは,3次元と7次元のベクトル空間に限られている。それ以外の空間では外積演算は存在しない。 クォータニオンについても似た事実がある。ハミルトンは3次元の複素数を求めて4次元の複素数,クォータニオンを発見した。その後の研究によって,クォータニオンのような超複素数が定義できるのは4次元と8次元(オクタニオンという)に限られることがわかっている。 すなわち, d/dt(ex ey ez) = (ω×ex ω×ey ω×ez) (1.2.7) この関係を図1.8に示す。 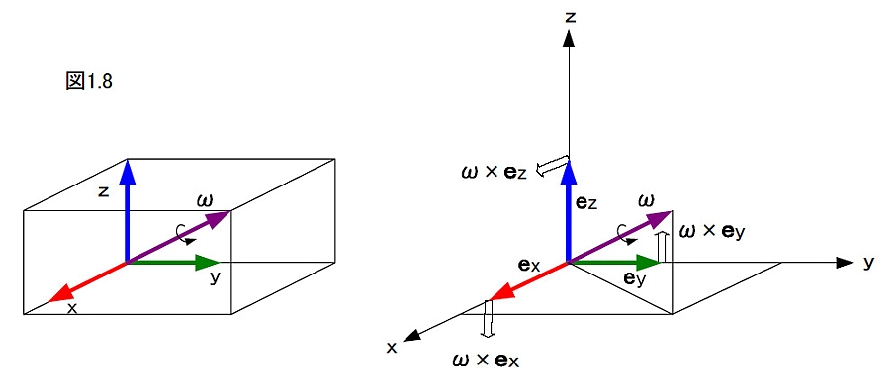 ラグビーセンサ座標系の原点を固定した運動,つまり回転運動では,ex,ey,ezの単位ベクトルはそれぞれ自らとωに直交する方向に変化速度を持つ。 |
||||||||||||||||||||
|
数学において、テイラー展開(テイラーてんかい、Taylor expansion)とは、無限回微分可能な関数 f(x) から、テイラー級数(テイラーきゅうすう、Taylor series)と呼ばれる、負冪の項を持たない冪級数 を得ることを言い、この級数がもとの関数 f(x) に一致するとき、f(x) はテイラー展開可能であるという。名称は数学者ブルック・テイラーに由来する。 厳密にはこの展開は x = a の近傍でのみ考えるものであり、x = a におけるテイラー展開とか、x = a のまわりでのテイラー展開などという。a = 0 のとき を特にマクローリン展開と呼ぶ |
(b)写像:so(3) →SO(3) スカラー変数x同次線形定係数微分方程式は定数aに対して以下のように解くことができる。 tは時刻でありX(0) はt=0でのxの初期値である。 これを多変数に拡張したものとして,ベクトル変数xの同次線形定係数方程式は定数行列Aに対して次のように解くことができるl。 ここで,eAtは次のような無限級数として定義される。 eAt = E +A t + A2/2! t2 + A3/3! t3 + ・・・・・ (1.2.10) (1.2.6)式は行列変数の微分方程式である。 いまωを定数とすると,(1.2.6)式は行列変数の線形定係数微分方程式である。したがって, となる。 nを単位ベクトル,ψをスカラーとして,ωt=nψと表し,次の関係 [n×]2 = n nT - |n|2E = n nT - E (1.2.12) [n×]3 = -[n×] (1.2.13) を用いると次の式が得られる。 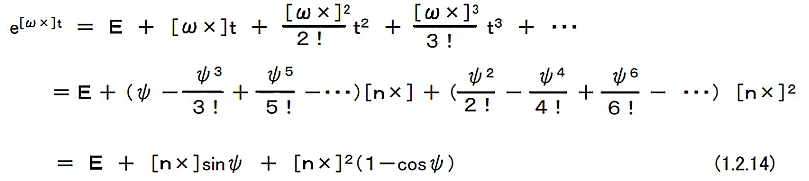 結果を(1.2.11)式に代入すると,以下の式を得る。 ここで,初期姿勢R(0)がグランド座標系に等しいとして,R(0)=Eとおいたものがロドリゲスの式である。 このようにR=e[n×]ψをマクローリン展開して整理したものがロドリゲスの式なる。 任意なRに対して,必ず,ωt=nψが存在し,つまり,どんなラグビーセンサ姿勢も1本の固定軸nの周りの1回の回転ψで表すことができる。 つまり,オイラーの定理だ。 注意することは,(1.2.6)式が積分できるのは,ωが定数の時であって,時間と共に変化する場合は,このような解析的な積分結果は存在しない。 とはいえ,落胆することは無い。 ωが定数とみなせる時間Δt内であれば,良いわけで,我々はこの点に注意して,座標変換を繰り返して,運動を求める。 |
||||||||||||||||||||
| (C)同次変換行列 ラグビーセンサの位置と姿勢の6自由度の変位について議論を進める。 図1.9の左側のように,はじめにラグビーセンサは,センサー座標系{A}がグランド座標系{O}と一致するようにな位置と姿勢にあった。 ラグビーセンサの内部の点Qはセンサー座標系で表されAqの位置にある。 点Qはラグビーセンサと一体になって運動するが,運動によってもAqは変化しない。 図1.9 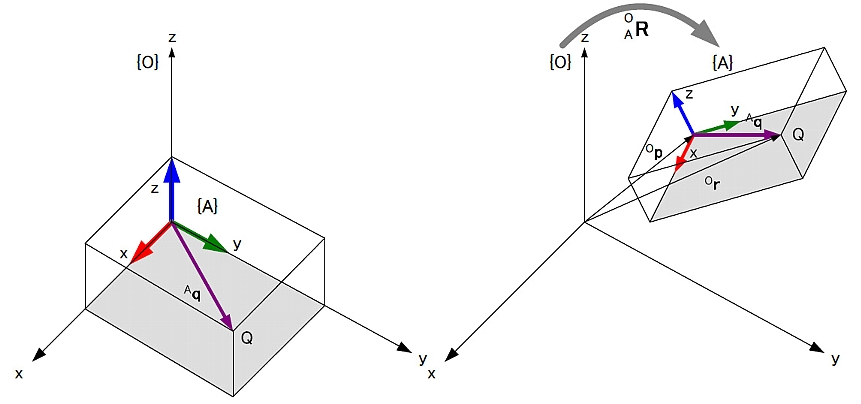 図1.9の右側のようにラグビーセンサの位置と姿勢が変化した。{A}の原点はOpの位置にある。ラグビーセンサの姿勢はAORである。 このとき{O}の原点から見た点Qの位置ベクトルOrは次のようになる。 Or = Op + AORAq (1.2.17) 同じ式を4×4に拡大した行列AOHを用いて次のようのに書くことができる。 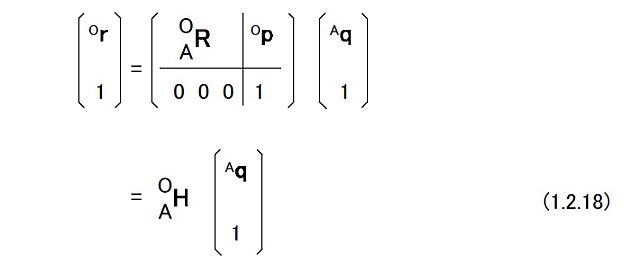 AOHを同次変換行列とよぶ。 AOHはセンサー座標系の原点の位置と姿勢の6自由度すべての情報を持っている。すなわち,AOH自身がラグビーセンサの位置と姿勢を表していると考えることができる。 図1.10では、n個のセンサー座標系{1}から{n}が存在し,その相対的な位置と姿勢が,ii-1H(i=1,・・・,n)で表されているとする。
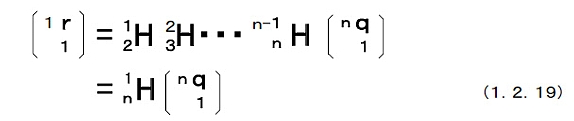 { i }の原点から{ i+1 }の原点に向かうベクトルを{ i }で記述したもの(計測したもの)をipとすると,i+1iHは次のようなものである。 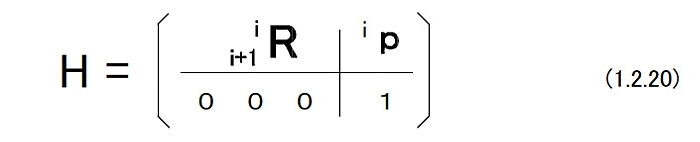 (1.2.19)式は同次変換行列のチェーンルールを意味している。 すなわち,  このような相対的な同次変換行列を左から右へ順番に掛けることによって絶対的な同次変換行列を計算することができる。同次変換行列の集合をSE(3)と書く。 i+1iHをi+1iRのアナロジーとしてとらえることが可能である。但し,i+1iHは直交行列では無い点に注意が必要だが,逆行列の計算には,割り算を使わずに,計算できる。 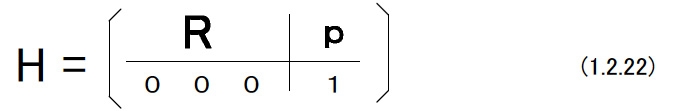 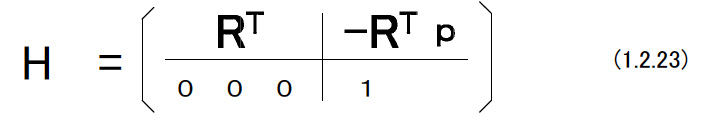 |
|||||||||||||||||||||
| (d)写像:se(3)→SE(3) 次のような6次元のベクトルξを作る。  ξ1,ξ2はそれぞれ3次元のベクトルとする。ξを用いて4×4行列|ξ×|を次のように定義する。 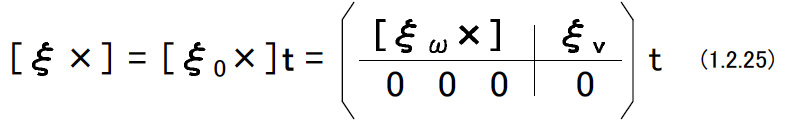 このような行列|ξ×|の集合はse(3)と記される。 so(3)からSO(3)への写像と同様に,se(3)からSE(3)への写像が存在し,指数関数で表される。すなわち, 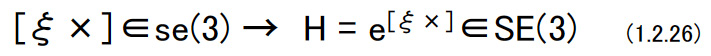 となる。 (1.2.26)式を導く。 はじめにマクローリン展開によって 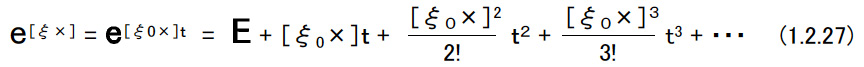 となる。ここで, 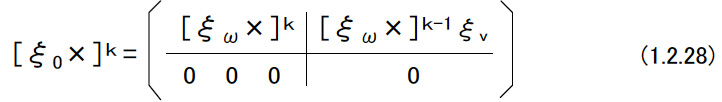 であることが簡単に確認できる。 この関係を(1.2.27)式に代入し,(1.2.14)式を考慮すると次式を得る。 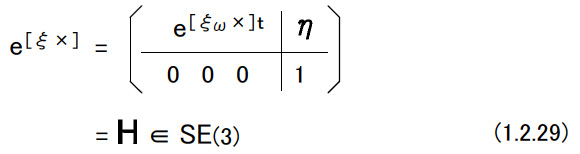 ここでηは次のようなベクトルである。 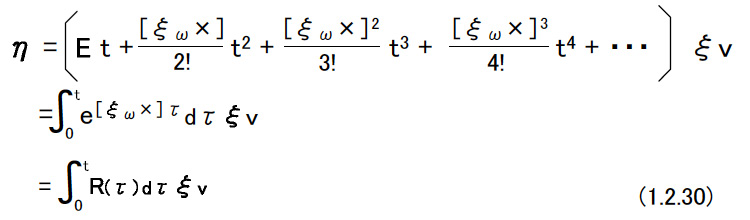 ξvが定義ならば,上式の積分の中に入ることができる。つまり,  である。下図のように,運動するR(τ)座標系(センサー座標系)での中で一定に見える速度ξvを絶対座標系(グランド座標系)したものをR(τ)ξvとし,これを時刻0からtまで積分したものがηである。 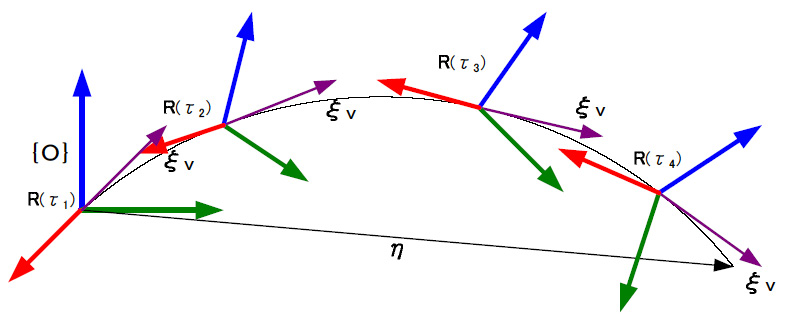 |
|||||||||||||||||||||
| (e)スクリューとツイスト 同次変換行列の微分 (1.2.22)式を時間で微分し,[ω×]=-R |